Proportions Harmonieuses : Le Secret des Artisans pour des Créations qui Ont de l’Âme

Ça fait des années que je suis dans le métier. J’ai touché au bois, à la pierre, et j’ai passé un temps fou à dessiner des espaces pour qu’ils soient à la fois pratiques et, surtout, agréables à l’œil. Au début, comme tout le monde, j’étais obsédé par la technique pure : l’angle de coupe parfait, la bonne pression sur le ciseau… C’est la base, on est d’accord. Mais mon ancien patron me répétait sans cesse : « La technique fait un bon ouvrier. La compréhension des proportions fait un artisan. »

Aujourd’hui, j’ai envie de vous partager un de ces fameux secrets d’atelier. Ce n’est pas une formule magique, loin de là, mais plutôt un guide. Un outil aussi essentiel pour moi que mon équerre. Il s’agit de la suite de Fibonacci et de son cousin, le Nombre d’Or. Vous en avez sûrement entendu parler, souvent avec des images de coquillages ou de galaxies. C’est fascinant, mais je veux vous montrer comment ces chiffres s’appliquent concrètement dans un meuble, un escalier ou une façade. Comment ils nous aident, nous les manuels, à créer un équilibre que l’œil adore, sans même qu’on sache pourquoi.

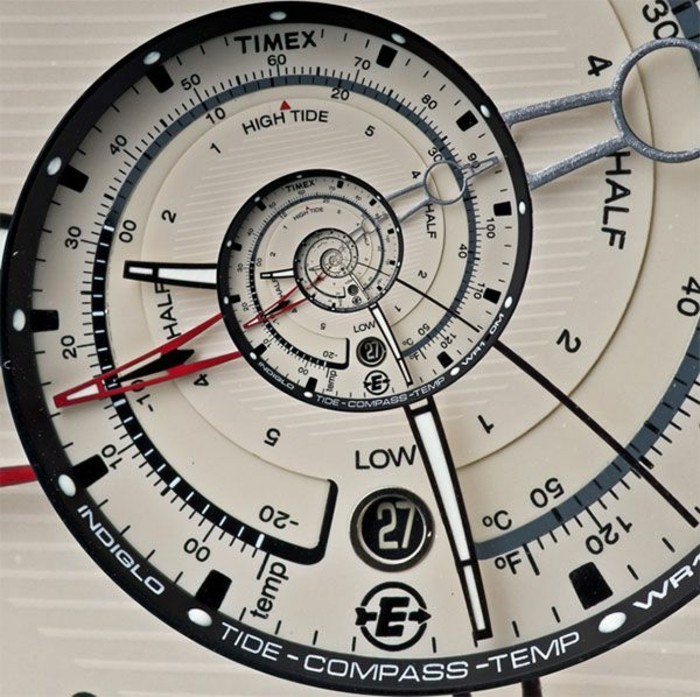
La mécanique toute simple derrière l’harmonie

Avant de sortir les outils, comprenons juste le principe. Et pas de panique, je ne suis pas prof de maths. Je vais vous expliquer ça comme on me l’a transmis à l’atelier, avec des mots simples.

La suite de Fibonacci est une série de nombres où chaque nouveau nombre est la somme des deux précédents. Ça donne : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34… et ça continue à l’infini. L’important n’est pas de retenir la suite par cœur, mais de voir ce qui se passe quand on divise ces nombres entre eux.

Regardez :

• 8 / 5 = 1,6
• 13 / 8 = 1,625
• 21 / 13 = 1,615…

Plus on avance, plus le résultat se rapproche d’un chiffre un peu spécial : environ 1,618. C’est lui, le fameux Nombre d’Or. C’est un rapport, une proportion, que notre cerveau trouve instinctivement équilibrée et plaisante.

Pourquoi ? Honnêtement, les théories sont nombreuses. La plus simple, c’est que la nature l’utilise partout : dans les spirales d’une pomme de pin ou le cœur d’un tournesol. Notre œil a donc appris à considérer ce modèle comme « normal » et harmonieux. En le reproduisant dans nos créations, on crée un sentiment de familiarité, de bien-être.

Astuce peu connue : Sortez une carte de crédit de votre portefeuille. Divisez sa longueur par sa largeur. Le résultat est incroyablement proche de 1,618. Vous avez un « rectangle d’or » avec vous en permanence !

L’erreur qui m’a tout appris

Au début de ma carrière, j’ai conçu et fabriqué une grande enfilade parfaitement symétrique. Deux portes de chaque côté, trois tiroirs au milieu, tout était millimétré. Le client était content, le meuble était fonctionnel. Mais moi, je le trouvais froid, sans vie, presque militaire. C’est en le regardant que j’ai enfin compris ce que mon maître voulait dire par « proportions ». La perfection technique ne suffit pas à donner une âme à un objet.

L’application à l’atelier : du plan à la matière

Bon, assez de théorie. Comment ça se passe en vrai ? Voilà des exemples concrets, tirés de chantiers.

Le cas d’une bibliothèque sur mesure

Un client voulait une grande bibliothèque pour un mur de 4 mètres de large sur 2,50 m de haut. Le réflexe du débutant ? Diviser les 4 mètres en caissons égaux. C’est simple, mais un peu ennuyeux visuellement.

Voici comment j’ai abordé le projet. J’ai pris la largeur totale, 400 cm, et je l’ai divisée par le Nombre d’Or : 400 / 1,618 ≈ 247 cm. J’ai donc dessiné une section principale de 247 cm et une section secondaire pour le reste, soit 153 cm. Pas besoin de logiciel 3D pour ça, un simple croquis sur un carnet suffit ! Cette division asymétrique crée tout de suite une dynamique, un intérêt visuel.

Ensuite, pour les étagères, au lieu de les espacer toutes de 30 cm, j’ai pioché dans la suite de Fibonacci : des niches basses de 21 cm pour les poches, des hauteurs de 34 cm pour les romans, et un grand espace de 55 cm pour les beaux livres d’art. Le résultat est un meuble qui a l’air vivant, rythmé. Il est imposant, mais il ne pèse pas sur la pièce. Le client m’a dit : « Je ne sais pas pourquoi, mais il est exactement comme il faut. »

Bon à savoir : Cette réflexion sur les proportions ne coûte rien de plus en matériaux. C’est du temps de conception, mais ça donne au meuble une valeur perçue bien supérieure.

Concevoir un escalier : l’équilibre entre esthétique et sécurité

Un escalier en colimaçon bien conçu suit souvent une courbe logarithmique, directement liée à ce rapport d’or. C’est ce qui lui donne cette fluidité, cette élégance naturelle.

Mais attention ! L’esthétique ne doit JAMAIS prendre le pas sur la sécurité. Il existe une règle de confort bien connue dans le métier pour les escaliers : le double de la hauteur d’une marche plus la largeur du giron (là où on pose le pied) doit être compris entre 60 et 64 cm. C’est une formule basée sur la longueur moyenne d’un pas, qui garantit que l’escalier est sûr et agréable à utiliser.

Le vrai savoir-faire, c’est de faire cohabiter la beauté de la spirale d’or avec la rigueur de cette règle. C’est un jeu de compromis constant entre l’idéal et la réalité.

Pour vous lancer : par où commencer ?

Pas besoin d’être un pro pour s’amuser avec ces principes. Vous pouvez les appliquer à des projets très simples à la maison.

Fabriquez votre propre outil pour moins de 5 €

Un excellent point de départ est de se fabriquer un « compas d’or ». C’est un petit outil qui maintient mécaniquement le rapport de 1,618. Prenez trois petites lattes de bois plat (environ 30 cm de long) et quelques vis papillon. Vous trouverez des plans et des tutos vidéo très simples en cherchant « fabriquer compas nombre d’or ». Tout le matériel se trouve pour quelques euros dans n’importe quel magasin de bricolage comme Castorama ou Leroy Merlin. Une fois que vous l’avez en main, baladez-vous chez vous et mesurez des objets : des livres, des cadres, des boîtes… C’est un vrai jeu !

Améliorez votre déco en 5 minutes

Vous voulez accrocher un tableau ? Oubliez le centre du mur. Utilisez la règle des tiers (une version simplifiée du Nombre d’Or). Imaginez votre mur divisé en trois, à la verticale et à l’horizontale. Placez le point d’intérêt de votre tableau sur l’une de ces lignes, ou à une intersection. L’effet est instantané, la composition respire.

Pour aménager un salon, au lieu de tout coller aux murs, créez un « bloc » principal (canapé, table basse, fauteuil) qui occupe environ 60% de la surface de la pièce, laissant les 40% restants plus aérés pour la circulation. L’équilibre est souvent bien meilleur.

D’ailleurs, n’oubliez pas que c’est un guide, pas une loi gravée dans le marbre. L’objectif est de former votre œil. Avec le temps, vous n’aurez plus besoin de mesurer, vous sentirez quand une proportion est juste.

La sécurité avant tout : les limites à ne pas franchir

Je ne le répéterai jamais assez : la beauté ne sert à rien si une création est dangereuse ou si une structure est fragile. C’est notre responsabilité numéro une.

Le piège classique, ce sont les escaliers « design » vus dans les magazines, avec des marches ultra-fines près du poteau central. C’est peut-être joli en photo, mais au quotidien, c’est une source de danger. Ne sacrifiez jamais un appui sûr pour un effet de style.

De même, vouloir une immense fenêtre pour respecter une proportion ne doit jamais vous faire toucher à un mur porteur sans l’avis d’un ingénieur structure. Les normes de construction sont là pour garantir la solidité des ouvrages, et les ignorer peut avoir des conséquences dramatiques.

Bref, soyez honnête avec vous-même. Dessiner une étagère, c’est un super projet. Concevoir un escalier, c’est un autre métier. Faire appel à un pro pour les travaux critiques, ce n’est pas un échec, c’est une preuve de sagesse.

En conclusion, ce fameux Nombre d’Or est un outil extraordinaire. Il nous relie à une longue tradition de bâtisseurs qui cherchaient, comme nous, à créer de la beauté et de l’harmonie. Mais ça reste un outil. Il ne remplace ni l’expérience, ni le bon sens, ni le respect des règles de sécurité. Je l’utilise comme une boussole, pas comme une carte détaillée. Il me donne une direction. Le chemin, c’est à moi de le tracer, avec mes mains, mon œil, et cette intuition que seules les années de pratique peuvent affiner.

Galerie d’inspiration

Le Modulor de Le Corbusier : L’architecte visionnaire a développé son propre système de proportions, le Modulor, basé sur la morphologie humaine et le Nombre d’Or. Il l’a utilisé pour concevoir des unités d’habitation, comme la Cité Radieuse à Marseille, où chaque élément, de la hauteur de plafond à la poignée de porte, est pensé pour être en harmonie avec l’Homme. Une application grandeur nature de la philosophie de l’article.

• Le canapé et la table basse : La longueur de votre table basse devrait idéalement mesurer environ deux tiers de la longueur de votre canapé pour un équilibre visuel.
• La hauteur des cadres : Accrochez vos œuvres d’art de sorte que leur centre soit à environ 1,60 m du sol – la hauteur moyenne du regard.
• Les tapis : Un tapis doit ancrer un espace. Assurez-vous qu’au moins les pieds avant de vos fauteuils et canapés reposent dessus, créant un rectangle harmonieux.

Le célèbre typographe Jan Tschichold a affirmé que les proportions de page basées sur le Nombre d’Or sont les plus belles et les plus fonctionnelles. On le retrouve dans la conception de nombreux livres anciens et modernes.

Peut-on appliquer ces proportions aux couleurs ?

Absolument. La règle du 60-30-10 en décoration est une simplification de ce principe d’équilibre. 60% pour votre couleur dominante (murs), 30% pour une couleur secondaire (mobilier, rideaux) et 10% pour une couleur d’accent (coussins, objets). Ce rapport crée une hiérarchie visuelle qui empêche l’espace de paraître plat ou chaotique, guidant l’œil naturellement.

Un outil, deux philosophies :

Le compas à proportion dorée : Un outil physique, souvent en laiton ou en bois, qui s’ouvre en maintenant le rapport de 1:1,618. Idéal pour les ébénistes, les sculpteurs et les dessinateurs qui travaillent la matière.

Le plugin pour logiciel : Des extensions pour des logiciels comme Figma, Sketch ou Adobe XD permettent d’appliquer des grilles basées sur le Nombre d’Or en un clic. Essentiel pour les designers d’interface et les graphistes.

L’un connecte la main à la matière, l’autre l’esprit au digital, mais le principe d’harmonie reste le même.

Au-delà du meuble, le jardin est un terrain de jeu idéal pour la suite de Fibonacci. Lors de la plantation de vivaces en massifs, essayez de les grouper par nombres impairs issus de la suite : 3, 5 ou 8 plants d’une même variété.

• Crée un effet plus naturel et moins rigide qu’un groupement par paires.
• Permet à l’œil de se poser sur un point central tout en appréciant l’ensemble.

On estime que les ouïes en forme de f des violons de Stradivarius suivent les proportions du Nombre d’Or, contribuant non seulement à leur beauté iconique mais aussi, selon certains luthiers, à leur acoustique exceptionnelle.

Cette perfection géométrique, appliquée au choix méticuleux de l’épicéa et de l’érable, est un exemple ultime où l’art, la science et l’artisanat se rencontrent pour créer un objet qui traverse les siècles.

L’erreur à éviter : confondre harmonie et symétrie. La symétrie pure peut être statique, voire ennuyeuse. L’harmonie basée sur le Nombre d’Or, elle, est dynamique. C’est une asymétrie équilibrée qui crée du mouvement et de l’intérêt. Pensez à un bonsaï : il n’est jamais symétrique, mais ses proportions lui confèrent un équilibre parfait.

• Une composition visuelle qui guide le regard sans effort.
• Un équilibre naturel entre les éléments et le vide.
• Une photo qui semble tout simplement « juste » et professionnelle.

Le secret ? La grille de la Règle des Tiers, une simplification directe du rectangle d’or, qui place les points d’intérêt sur des lignes de force pour un impact maximal.

Un meuble iconique comme le fauteuil Eames Lounge Chair, conçu par Charles et Ray Eames pour Vitra, est une leçon de proportions. La hauteur du dossier par rapport à celle de l’assise, l’inclinaison, le rapport entre le fauteuil et son ottoman… rien n’est laissé au hasard. C’est cet équilibre invisible qui justifie son statut d’œuvre d’art fonctionnelle.

Faut-il suivre le Nombre d’Or à la lettre ?

Non, et c’est là que l’artisan se distingue du technicien. Ces proportions sont un guide, pas une loi. Elles servent à éduquer l’œil et à donner un point de départ. L’intuition, l’expérience et la nature du matériau (le veinage d’un bois, la texture d’une pierre) doivent toujours avoir le dernier mot pour qu’une création ait une âme.

« La géométrie peut produire sans peine, à partir de ses figures, les fondements de l’architecture et de tout ce qui se meut au moyen de la machine. » – Albrecht Dürer, 1525

La tendance du design biophilique, qui vise à reconnecter nos intérieurs à la nature, s’appuie instinctivement sur ces principes. En intégrant des formes, des motifs et des matériaux naturels (bois brut, pierre, plantes aux feuilles spiralées), on importe indirectement les proportions harmonieuses que la nature a perfectionnées depuis des millions d’années.

Point important : Le vide est une matière. En design d’intérieur ou en graphisme, l’espace négatif (le blanc) est aussi crucial que les objets eux-mêmes. La répartition de ces vides doit aussi suivre une logique de proportion. Un espacement harmonieux entre les meubles ou les paragraphes d’un texte crée une sensation de luxe et de clarté.

Pensez à la hiérarchie de vos textes. Une mise en page agréable suit souvent la suite de Fibonacci pour définir les tailles de police.

• Titre principal : 34pt
• Titre de section : 21pt
• Corps de texte : 13pt

Ce rapport crée une lecture fluide et intuitive, où l’importance de chaque élément est immédiatement perceptible.

Pas besoin d’outils complexes pour commencer. Prenez n’importe quel objet rectangulaire, comme un livre ou un smartphone. Mesurez sa longueur et sa largeur. Divisez la plus grande mesure par la plus petite. Si le résultat est proche de 1,618, vous tenez un rectangle d’or. Un exercice simple pour entraîner votre œil à reconnaître l’harmonie.

Le logo d’Apple est souvent cité comme un exemple parfait du Nombre d’Or. Si le design final est incroyablement équilibré, son créateur, Rob Janoff, a expliqué que les proportions harmonieuses résultaient plus d’une recherche esthétique intuitive que d’une application mathématique stricte.

Cela confirme une idée chère aux artisans : la connaissance des règles permet parfois de les appliquer instinctivement, sans même avoir besoin de les mesurer.

Un design bien proportionné est un design intemporel. Les modes passent, les couleurs changent, mais une forme harmonieuse reste agréable à l’œil. Investir dans un meuble dont les proportions sont justes, c’est choisir un objet qui ne se démodera pas, qui traversera les années avec grâce. C’est l’essence même de la durabilité : acheter moins, mais mieux.

• Les hauteurs des tiroirs d’une commode.
• Le ratio entre la largeur du plateau et la hauteur des pieds d’une table.
• La division d’une bibliothèque en sections asymétriques mais équilibrées.

La clé ? Utiliser les nombres de la suite (3, 5, 8, 13, 21…) comme unités de mesure pour créer une rythmique visuelle sur l’ensemble de la pièce.

D’où vient le terme « Divine Proportion » ?

C’est le moine et mathématicien italien Luca Pacioli qui l’a popularisé dans son traité « De divina proportione » en 1509. L’ouvrage, illustré par son ami Léonard de Vinci, élevait ce ratio mathématique au rang de principe esthétique et quasi-mystique, le considérant comme une manifestation de la perfection divine dans la création.

Peinture à l’huile : La texture onctueuse d’une peinture à l’huile de qualité, comme celles de la marque Sennelier, permet de créer des empâtements dont l’ombre et la lumière jouent avec les proportions de la toile.

Marbre de Carrare : Le veinage imprévisible de ce marbre italien offre un contrepoint organique parfait à la rigueur géométrique d’un plan de travail ou d’un sol aux dimensions calculées.

L’harmonie naît souvent de la rencontre entre une structure pensée et un matériau vibrant.

Si le Parthénon est l’exemple canonique, des études récentes montrent que ses proportions s’écartent souvent du Nombre d’Or exact. Les architectes grecs utilisaient plutôt des ratios de nombres entiers simples (comme 4:9) et des corrections optiques subtiles pour atteindre une perfection visuelle perçue, et non purement mathématique. L’harmonie est aussi une affaire d’adaptation à la perception humaine.

8, 13, 21… Ces nombres de la suite de Fibonacci se retrouvent dans le nombre de pétales de nombreuses fleurs. Les marguerites, par exemple, ont souvent 21, 34 ou 55 pétales.

Avez-vous déjà ressenti un sentiment de calme et de plénitude dans certains lieux, comme la nef d’une cathédrale ou une pièce conçue par un grand architecte ? C’est souvent l’effet subconscient des proportions harmonieuses. Notre cerveau, câblé pour reconnaître ces schémas naturels, interprète cet ordre visuel comme un signal de sécurité et de bien-être, apaisant le système nerveux.

Projet pour le weekend : fabriquez une petite étagère murale en chêne en utilisant le rapport d’or. Créez un rectangle principal (ex: 80cm x 49.4cm). Puis, divisez l’espace verticalement avec une seule tablette en suivant le même ratio (à 49.4cm ou 30.6cm du bord). Vous obtiendrez un carré et un plus petit rectangle d’or, une composition simple mais profondément satisfaisante.