Presque tout le monde fait une erreur. Quel est le résultat ?

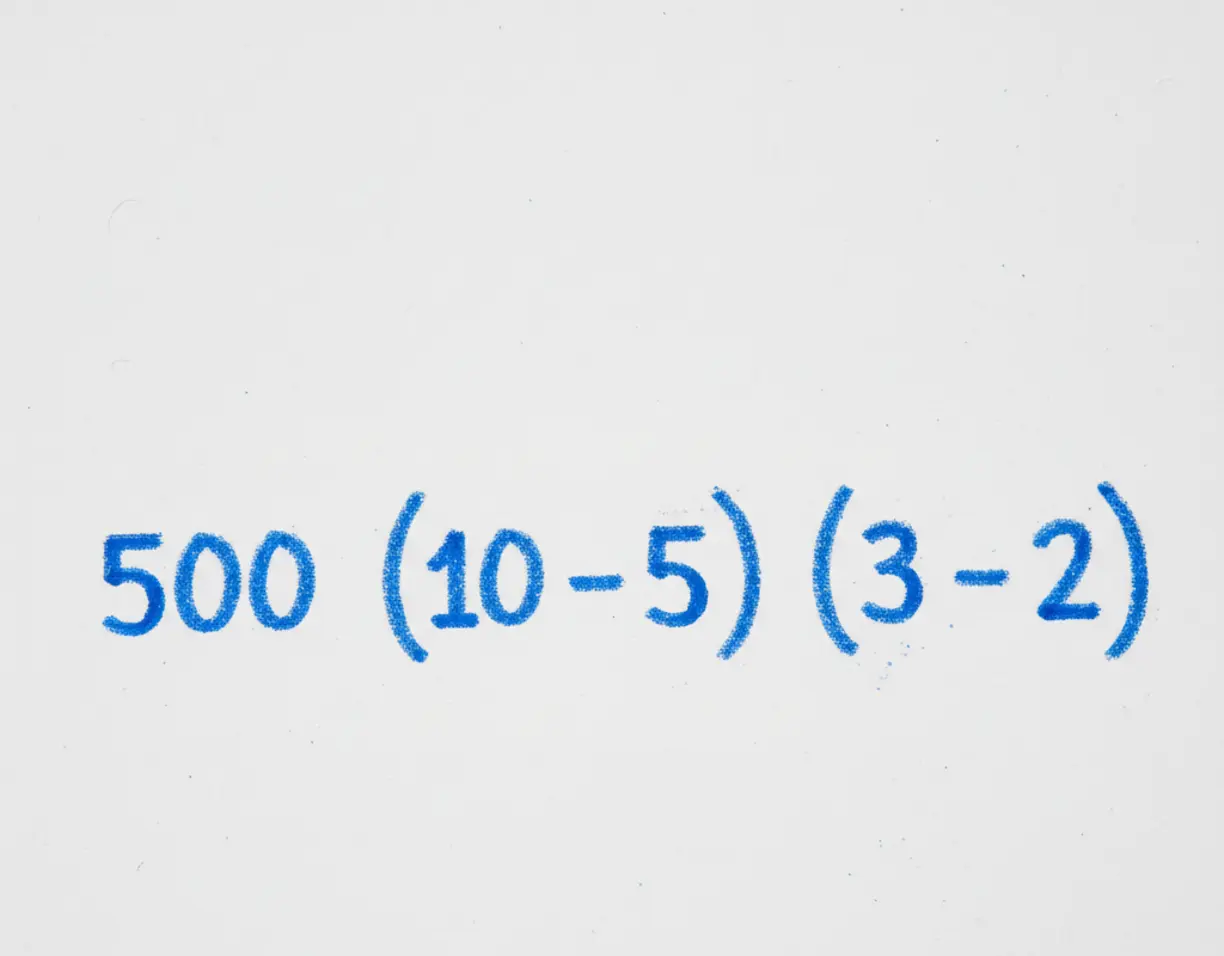
Sur les réseaux sociaux, dans les discussions familiales ou même au bureau, une simple équation mathématique est devenue un véritable champ de bataille intellectuel. La voici : 8 ÷ 2 (2 + 2) = ?. À première vue, l’opération semble relever du niveau collège. Pourtant, elle sème la discorde et révèle des failles surprenantes dans notre raisonnement logique. La grande majorité des gens obtiennent deux résultats différents, mais un seul est correct. Avant de continuer, prenez un instant pour la résoudre. Votre réponse est-elle 1 ou 16 ?

Si vous avez répondu 1, vous faites partie d’un groupe très large. Le raisonnement est souvent le suivant : on résout d’abord la parenthèse (2 + 2), ce qui donne 4. L’équation devient 8 ÷ 2(4). L’intuition pousse alors à voir le 2(4) comme un bloc inséparable, une multiplication prioritaire liée à la parenthèse. On calcule donc 2 x 4 = 8, et l’équation finale devient 8 ÷ 8, soit 1. C’est une erreur de perception courante, encouragée par la proximité visuelle des chiffres.

Si vous avez répondu 16, félicitations, vous avez appliqué la bonne méthode. Mais la simplicité du résultat cache une règle fondamentale souvent oubliée, un vestige de nos cours de mathématiques qui s’est érodé avec le temps.

La règle oubliée qui change tout

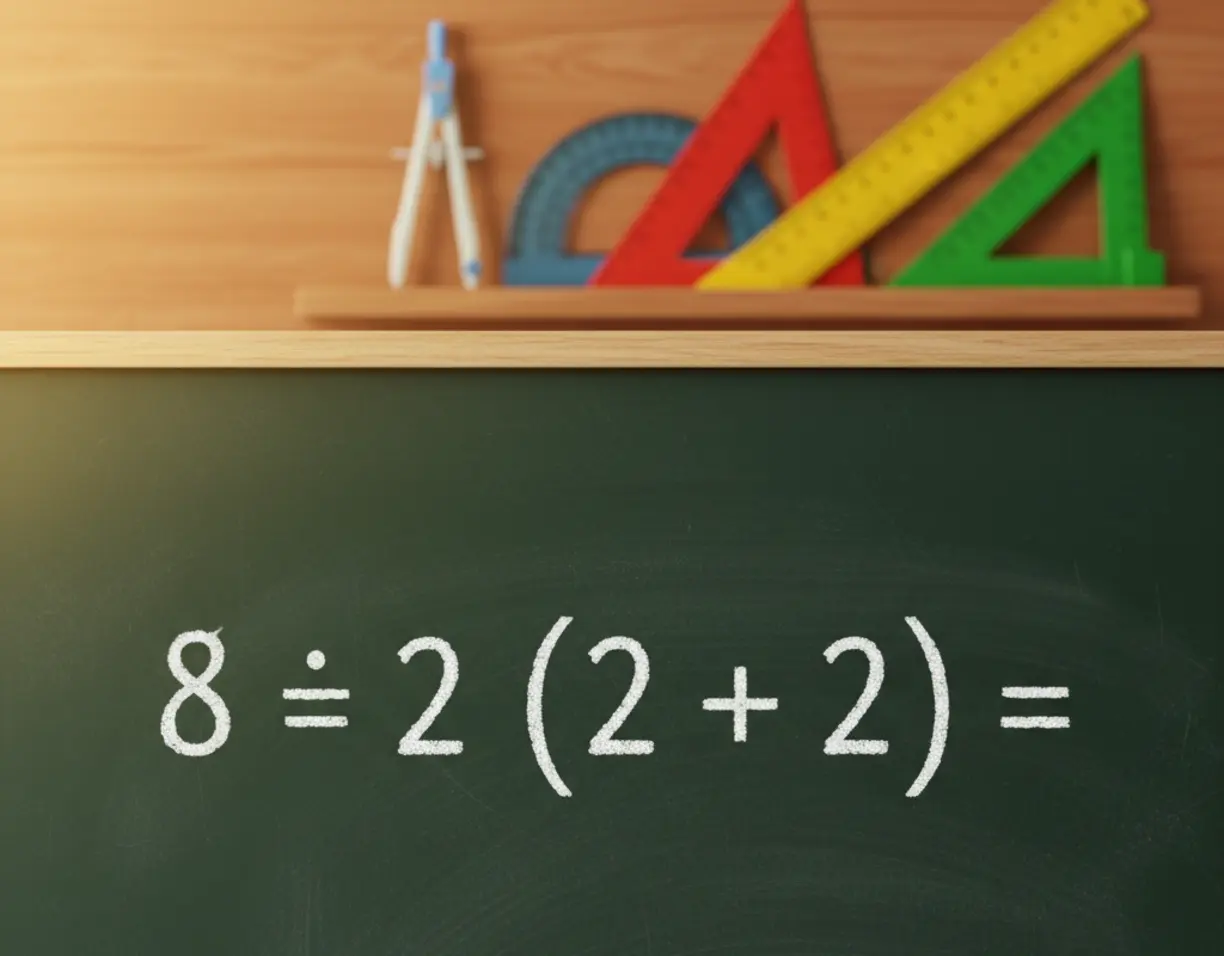
Le piège ne réside pas dans la complexité du calcul, mais dans l’ordre des opérations. En France et dans de nombreux pays, on apprend la règle PEMDAS (Parenthèses, Exposants, Multiplication et Division, Addition et Soustraction). Cette hiérarchie est la clé de voûte de l’arithmétique moderne, une convention universelle qui permet aux scientifiques, ingénieurs et informaticiens du monde entier de parler le même langage mathématique.

L’erreur la plus fréquente concerne le duo « Multiplication et Division ». L’acronyme PEMDAS peut laisser penser que la multiplication vient toujours avant la division. Or, ce n’est pas le cas. La multiplication et la division ont le même niveau de priorité. Lorsqu’elles se suivent dans une équation, la règle est de les effectuer dans leur ordre d’apparition, de gauche à droite. C’est ce détail crucial qui fait toute la différence.

Revenons à notre équation : 8 ÷ 2 (2 + 2).

• 1. Parenthèses : (2 + 2) = 4. L’équation devient : 8 ÷ 2 x 4. Notons que 2(4) est une notation implicite pour 2 x 4.
• 2. Multiplication et Division (de gauche à droite) : C’est ici que tout se joue. La première opération en partant de la gauche est la division. On doit donc calculer 8 ÷ 2 en premier, ce qui donne 4.
• 3. Suite du calcul : L’équation est maintenant 4 x 4.
• 4. Résultat final : 4 x 4 = 16.

Le résultat correct est donc 16. L’ambiguïté de l’écriture, sans un signe explicite de multiplication (x), est volontairement conçue pour induire en erreur notre cerveau, qui cherche des raccourcis et regroupe instinctivement le ‘2(4)’ comme une seule entité.

Plus qu’un calcul, un reflet de notre pensée

Pourquoi un problème si simple devient-il un phénomène viral, générant des millions de commentaires enflammés ? La réponse se situe à l’intersection de la psychologie cognitive et de la culture numérique. Notre cerveau est programmé pour l’efficacité, utilisant ce que le psychologue Daniel Kahneman appelle la « Pensée de Système 1 » : rapide, intuitive et automatique. Face à 2(4), ce système voit un tout cohérent et le traite en priorité, court-circuitant la « Pensée de Système 2 », plus lente, délibérée et logique, qui se rappellerait la règle de gauche à droite.

Ce type de casse-tête prospère sur les plateformes comme Facebook, X (anciennement Twitter) ou TikTok car il est parfaitement adapté à leurs algorithmes. Il ne demande qu’un investissement minimal de temps, provoque un engagement émotionnel fort (le désir d’avoir raison, la surprise de se tromper) et incite au débat. Chaque commentaire, qu’il soit bon ou mauvais, nourrit la visibilité de la publication. C’est une mécanique d’engagement à faible coût mais à haut rendement.

Ce phénomène soulève également des questions sur l’enseignement des mathématiques. Si une règle aussi fondamentale est oubliée par une si grande partie de la population adulte, cela témoigne-t-il d’un enseignement trop axé sur la mémorisation ponctuelle plutôt que sur la compréhension profonde des concepts ? En France, la maîtrise des opérations de base fait partie du « socle commun de connaissances, de compétences et de culture », mais la pratique régulière, essentielle à l’ancrage des savoirs, se perd souvent après le cursus scolaire.

En fin de compte, cette petite équation est un miroir. Elle ne teste pas vraiment notre intelligence, mais plutôt notre rigueur, notre attention aux détails et notre capacité à résister aux automatismes de pensée. Dans un monde saturé d’informations où les conclusions rapides et les réactions instinctives sont devenues la norme, prendre le temps de décomposer un problème, de se souvenir des règles et de les appliquer méthodiquement est une compétence plus précieuse que jamais. Ce n’est pas seulement une question de mathématiques, mais une leçon de pensée critique.